Gambles, Rays & Cones

Gambles

class murasyp.gambles.Gamble(data={})

Gambles map states to utility payoffs

This class derives from Vector, so its methods apply here as well.

What has changed:

• There is a new constructor. If data is not a Mapping, but is a Iterable Hashable Container, then its so-called indicator function is generated.

  >>> assert Gamble('abc') == Gamble({'a': 1, 'c': 1, 'b': 1})
  >>> assert Gamble({'abc'}) == Gamble({'abc': 1})
  

• A gamble’s domain can be cylindrically extended to the cartesian product of its domain and a specified Set.

  >>> assert (
  ...     Gamble({'a': 0, 'b': -1}) ^ {'c', 'd'} ==
  ...     Gamble({('b', 'c'): -1, ('a', 'd'): 0,
  ...             ('a', 'c'): 0, ('b', 'd'): -1})
  ... )
  

bounds()

The minimum and maximum values of the gamble

returns:the minimum and maximum values of the gamble rtype:a pair (tuple) of Fraction

>>> Gamble({'a': 1, 'b': 3, 'c': 4}).bounds()
(Fraction(1, 1), Fraction(4, 1))
>>> Gamble({}).bounds()
(0, 0)

scaled_shifted()

Shifted and scaled version of the gamble

returns:a scaled and shifted version 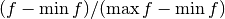of the gamble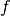 rtype:Gamble

>>> assert (
...     Gamble({'a': 1, 'b': 3, 'c': 4}).scaled_shifted() ==
...     Gamble({'a': 0, 'c': 1, 'b': '2/3'})
... )

Note

None is returned in case the gamble is constant:

>>> assert Gamble({'a': 2, 'b': 2}).scaled_shifted() == None

norm()

The max-norm of the gamble

returns:the max-norm 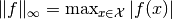of the gamble 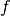rtype:Fraction

>>> Gamble({'a': 1, 'b': 3, 'c': 4}).norm()
Fraction(4, 1)

normalized()

Max-norm normalized version of the gamble

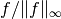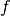
returns:a normalized version of the gamble rtype:Gamble

>>> assert (
...     Gamble({'a': 1, 'b': 3, 'c': 4}).normalized() ==
...     Gamble({'a': '1/4', 'c': 1, 'b': '3/4'})
... )

Note

None is returned in case the the gamble’s norm is zero.

>>> Gamble({'a': 0}).normalized() == None
True

Rays

class murasyp.gambles.Ray(data={})

Rays directions in gamble space

This class derives from Gamble, so its methods apply here as well.

What has changed:

• Its domain coincides with its support and it is max-normalized.

  >>> assert Ray({'a': 5, 'b': -1, 'c': 0}) == Ray({'a': 1, 'b': '-1/5'})
  >>> assert Ray({'a': 0}) == Ray({})
  

• Ray-arithmetic results in gambles (which can be converted to rays).

  >>> r = Ray({'a': 1,'b': -2})
  >>> assert .3 * r * r + r / 2 == Gamble({'a': '13/40', 'b': '-1/5'})
  

Cones

class murasyp.gambles.Cone(data=[])

A frozenset of rays

type data:a non-Mapping Iterable Container of arguments accepted by the Ray constructor.

>>> assert (
...     Cone([{'a': 2, 'b': 3}, {'b': 1, 'c': 4}]) ==
...     Cone({Ray({'a': '2/3', 'b': 1}), Ray({'c': 1, 'b': '1/4'})})
... )
>>> assert (
...     Cone('abc') ==
...     Cone({Ray({'a': 1}), Ray({'b': 1}), Ray({'c': 1})})
... )
>>> assert (
...     Cone({'ab', 'bc'}) ==
...     Cone({Ray({'c': 1, 'b': 1}), Ray({'a': 1, 'b': 1})})
... )

This class derives from Polytope, so its methods apply here as well.

Todo

test all set methods and fix, or elegantly deal with, broken ones